Economic Scenario Generators

At Annuity Risk, we offer a state-of-the-art Economic Scenario Generator that produces market consistent and risk neutral scenarios for equities, risk-free interest rates, and corporate bond rates. Our ESG can model correlations between economic variables comprehensively and accurately. Moreover, we analyze the insurer’s experience data to extract parameters that mimic their own policyholders' behavior and rates setting program, and then validate those scenarios.

Economic Scenario Generators

Economic Scenario Generators (ESGs) are used for generating economic scenarios that enable risk-neutral valuation of annuities and life insurance policies. Economic scenarios can be most easily visualized as a set of possible future states of existence, expressed via projected time series of equity index levels (hence called equity paths) or future interest rate curves.

More recently, Economic Scenarios have gained popularity in the valuation of Market Risk Benefits (MRBs)** as per FASB’s new Long Duration Targeted Improvements to the valuation and reserving of annuities.

As one may imagine, just about any hypothetical projected (future) time series of equity paths can be considered economic scenarios.

So, what key properties that we are looking for in the economic scenarios to consider them fit for the valuation of MRBs?

Stochastic

Economic scenarios are generated stochastically using Monte Carlo simulations and model parameters. The output of ESG is equity paths or interest rate paths. Using observed market inputs (traded prices of treasury bonds, interest rate derivatives, equity derivatives etc.) and models of interest rate and equity valuation, risk-neutral model parameters are calibrated.

Market Consistent

Economic scenarios should be consistent with the market conditions that prevailed on a particular valuation date. So, if the equity market was very volatile (large price fluctuations) on the valuation date, the economic scenarios should reflect that. If the yield curve was downward sloping, the economic scenarios should reflect that too.
In fact, if you calculate the price of a call option using such market-consistent economic scenarios, this calculated price should be close to the actual traded price of that option on that market date. A multitude of such tests are applied to economic scenarios to evaluate whether they are market consistent. Once this set of economic scenarios passes these tests, they are deemed market-consistent economic scenarios, and are now fit for valuation.

Correlations

Not only should the economic scenarios be market-consistent, they should also somehow reflect the implied linkages and correlation between variables such as interest rates and volatility. The ability to model complex relationships between economic variables (eg. interest rates, policyholder behavior and equity market outcomes) and the ability to price contingent cash flows are the two key advantages of using economic scenarios over analytic models. These two are also the main reasons behind regulatory agencies’ interest in ESGs. A limited number of such complex correlations can be modeled into the economic scenarios, and calibrated through a special algorithm that is referred to as a cascade structure. Cascade Structure helps capture dependency between model variables (such as between price return and dividend yield in stocks).

Risk Neutral

The terms market-consistent and risk-neutral are often used interchangeably in actuarial writings. However, here we are referring to the actual, technical meaning of risk-neutrality of economic scenarios, which means that the expected return implied by a set of scenarios should be the same as the expected return on a risk-free asset. Risk-neutrality is just an assumed simplification and not a reality. For instance, risk neutrality would suggest that a policyholder allocating her policy balance into fixed rate allocation vs equity indexed allocation would yield the same return, but that has not been true given the historical data. Using this risk-neutral framework does not render the model outcomes disjointed from reality. The validation of risk-neutrality is typically done via a martingale test. For risk-neutral scenarios that are used for pricing derivatives (options, swaps, futures, etc.), the scenarios also need to be arbitrage-free.

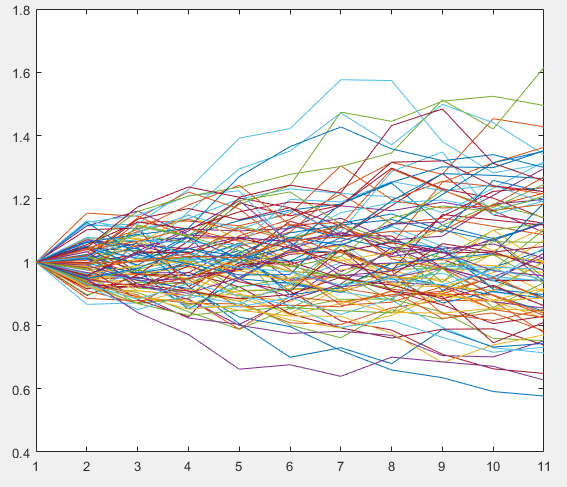
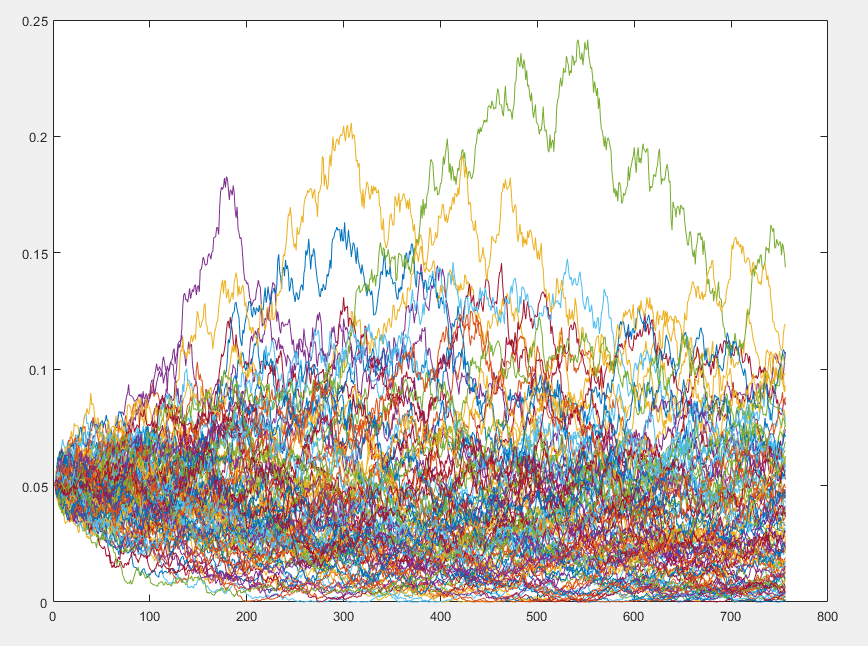
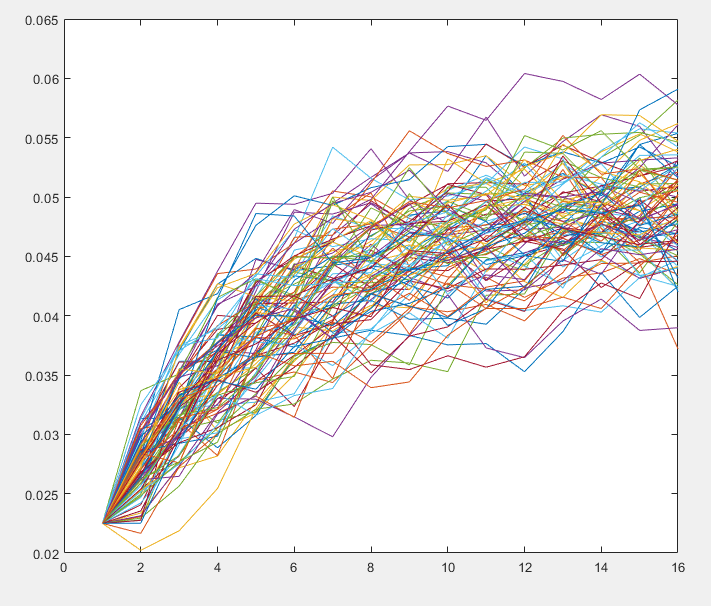
Models for Interest Rates and Equities

Almost all economic scenario generators used in life insurance and annuity industry need to generate risk free interest rates and equity paths. Most commonly used interest rate models are Nelson-Siegel, Hull-White and Cox-Ingersoll-Ross (CIR). The most commonly used equity model is the Black Scholes model, which assumes constant and flat volatility (same volatility for all tenors). Heston model incorporates stochastic volatility, while Bates model allows for both stochastic volatility and price jumps.

At Annuity Risk, our proprietary ESG covers the following models:

Black Scholes (Equity) Model
Heston (Equity) Stochastic Volatility Model
Bates (Equity) Stochastic Volatility with Jumps Model
Hull-White Interest Rates Model
Nelson Siegel Interest Rates Model
Cox-Ingersoll-Ross Interest Rates Model

Understanding Risk-Neutral Parameters, Models and Monte Carlo Data

Let’s use a very simple ‘toy’ example for understanding this process of generating economic scenarios.

Let’s assume that we are analyzing newborn human baby weights. We further choose Normal distribution as our model, and we gather actual data on newborn weights from nearby hospitals. Now, normal distribution has two key parameters – mean and variance – which we need to fit to the hospital data. So, using actual data and the model (normal distribution), we find the mean weight and standard deviation of newborns. And, let’s further assume that these values happen to be 7 pounds (mean weight) and 1 pound (standard deviation). So, now, these two values will be our ‘risk-neutral’ parameters.

The next step is to use these risk-neutral parameters, the model of normal distribution and a random number generator (to introduce stochastic noise, similar to Monte Carlo) to generate new values of newborn weights. The statistical properties of this synthetic data will be very similar to those of the actual (hospital) data. The economic scenarios generated by an ESG are merely a more complex version of this synthetic weight data we just generated using our toy example.

** Market Risk Benefits
Market Risk Benefit (MRB) means a contract feature that provides a benefit to the policyholder and also exposes the insurer to some form of market risk. For instance, by selling equity indexed annuities, insurers accept market risk and consequently provide a benefit to the policyholder. This benefit is not life contingent, and is significant, and contingent on market forces. So, if equities gain value, the policyholder gets the benefit of higher returns (higher interest rates). But if equities lose value, the policyholder is shielded from the risk by the insurer.

Email: info@annuityrisk.com
Phone: +1 646-535-4245

7659 Mall Road #1004, Florence, KY 41042